前回は、551の豚まんを例に「因果推論」とは何かを考えてみました。今回はRCTと呼ばれる手法を用いた因果関係の求め方を紹介します。
関連:因果推論のすすめ!!
RCT(ランダム化比較実験)とは?
1人なら同時に観測できなくても、集団なら同時に観測できるのではないかと考えて生み出されたのが、ランダム化比較実験(Randomized Controlled Trial)と呼ばれる実験です。
「ABテスト」が馴染み深いかもしれません。ただし、厳密な意味でABテストはRCTでは無いと言う人もいます。理由は後述します。
話は逸れますが、2019年のノーベル経済学賞は「世界の貧困を改善するための実験的アプローチに関する功績」として、RCTを採用し、効果的な貧困政策を検証するアビジット・バナジー教授らが受賞しました。
RCTを「集団なら同時に観測できる」と説明しました。2つの同質な集団に「551の豚まんがあるとき」「551の豚まんがないとき」を体験して貰い、その結果を観察するのです。
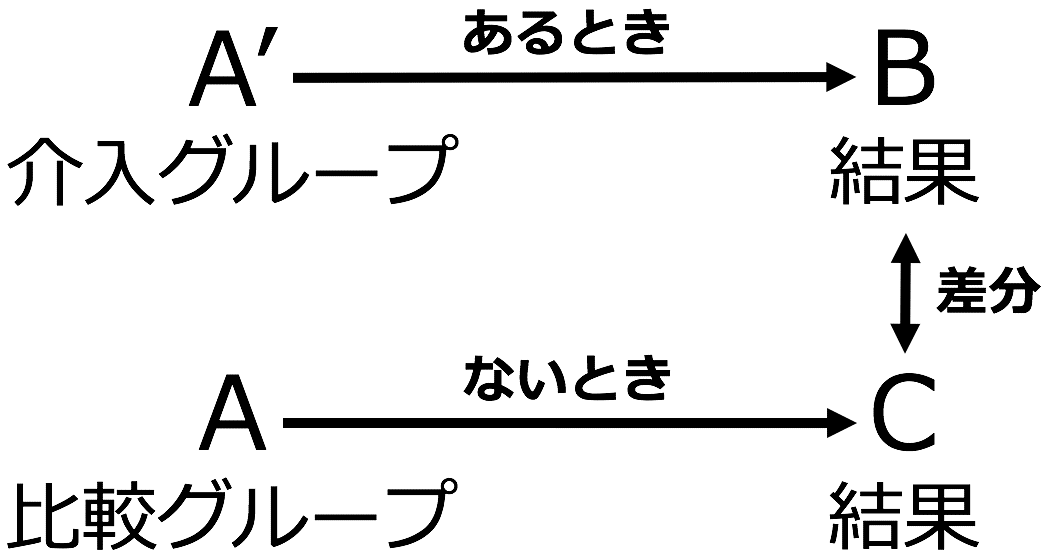
比較グループは「原因」が無い状態、つまり「551の豚まんがないとき」です。介入グループはわざと「原因」がある状態を作っていて、つまり「551の豚まんがあるとき」です。
比較グループ・介入グループにN人いて、同時に「551の豚まんがあるとき」「551の豚まんがないとき」を体験して貰い、その結果現れた差分の平均値を「平均介入効果」と表現します。
「平均介入効果」こそ、原因がもたらした結果だと言えるでしょう。
ABテストでは、複数のランディングページ(介入グループ)を用意して、どれがCVRが高いかなんて比較しますよね。平均介入効果のもっとも高いページを探しているのと同義なんです。
ただ、RCTには厳格なルールが設けられます。比較グループ・介入グループ共に同質の集団である必要があります。「1人なら無理でも複数なら」という前提に立つので、言い換えると「複数は1人のように同質」である必要があるのです。
比較グループは551の豚まんが好きで、介入グループは551の豚まんが嫌いなら、どちらも笑顔にはなりません。とはいえ「551の豚まんがあっても笑顔にならない」とは言えません。グループが同質では無いからです。
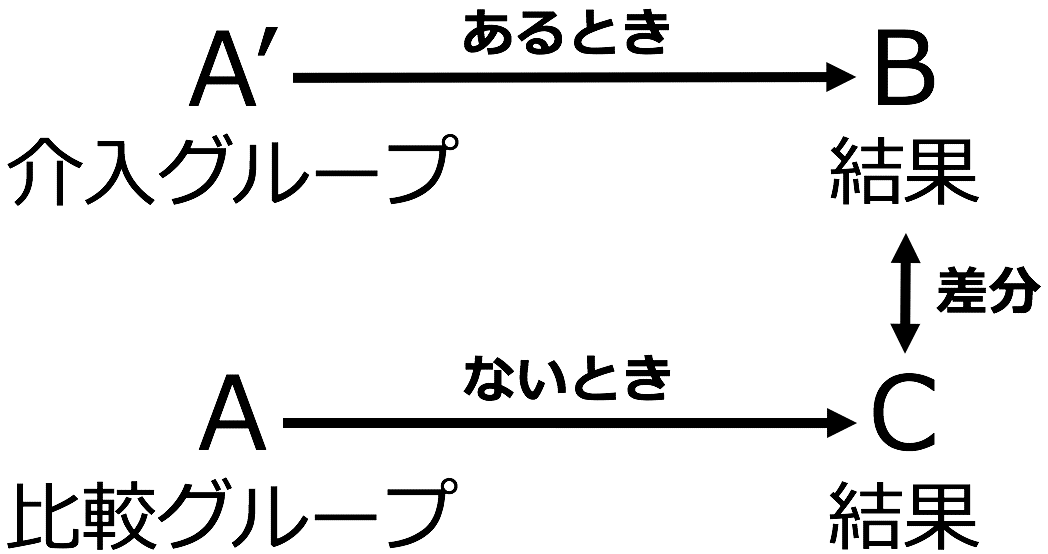
AにしろA’にしろ「介入のある・無し」以外に違いは考えられない、という前提に立つのがRCT(ランダム化比較実験)です。
このあたりが、因果関係の証明にどれほどビッグデータがあっても意味が無いと言われる理由ですね。まさに「実験」です。実験じゃないデータは使えないんですよね…。
ABテストが厳密な意味で「ランダム化比較実験なのか?」と疑問を呈されるのは、AとA’が本当に同質なのかが確認しようが無い点です。
以前、某健康食品系のABテストで「最初は機能ベネフィットを謳うBのCVRが相対的に高かったのに、やがて健康な自分の格好良さを強調したCが上回ったのは何故だろう?」という案件を手伝った機会があります。
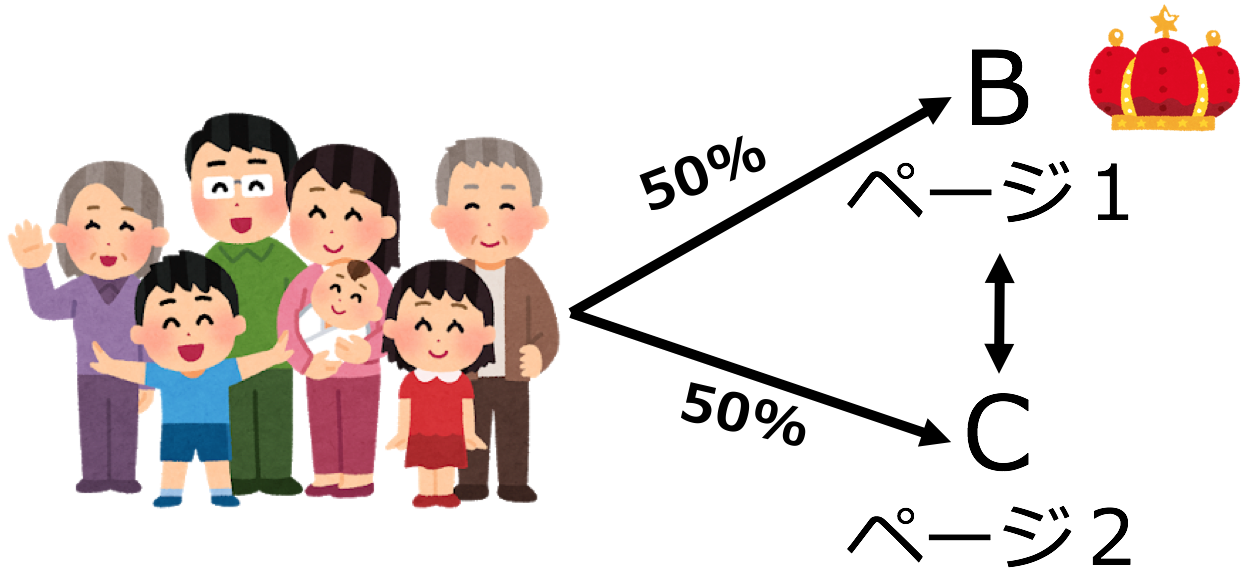
いろいろデータを触った結果、BのCVRが高い頃と、CのCVRが高い頃のユーザー層は同質とは言えないのではないか?という仮説に至りました。残念ながら証明はできませんが。
最初は機能ベネフィットに興味・関心を持つ層が広告をクリックし、それぞれ異なるランディングページに飛ばされていたのだろうけど、やがて少しずつ「健康になった後の自分」に興味・関心を持つ層が増えたのなら、現象の説明はできます。
ABテストをするにしても、期間を決めたり、上限人数を決めたり、出稿する媒体を気にしたり、いろいろ考えないといけないなーと感じた次第です。












